Stand: 08.09.2025
TL;DR
Die boolesche Algebra ist ein fundamentales Konzept in der Informatik und Mathematik, das auf den Operationen AND, OR und NOT basiert. In diesem Guide werden die Grundlagen, Anwendungen und Beispiele ausführlich erklärt.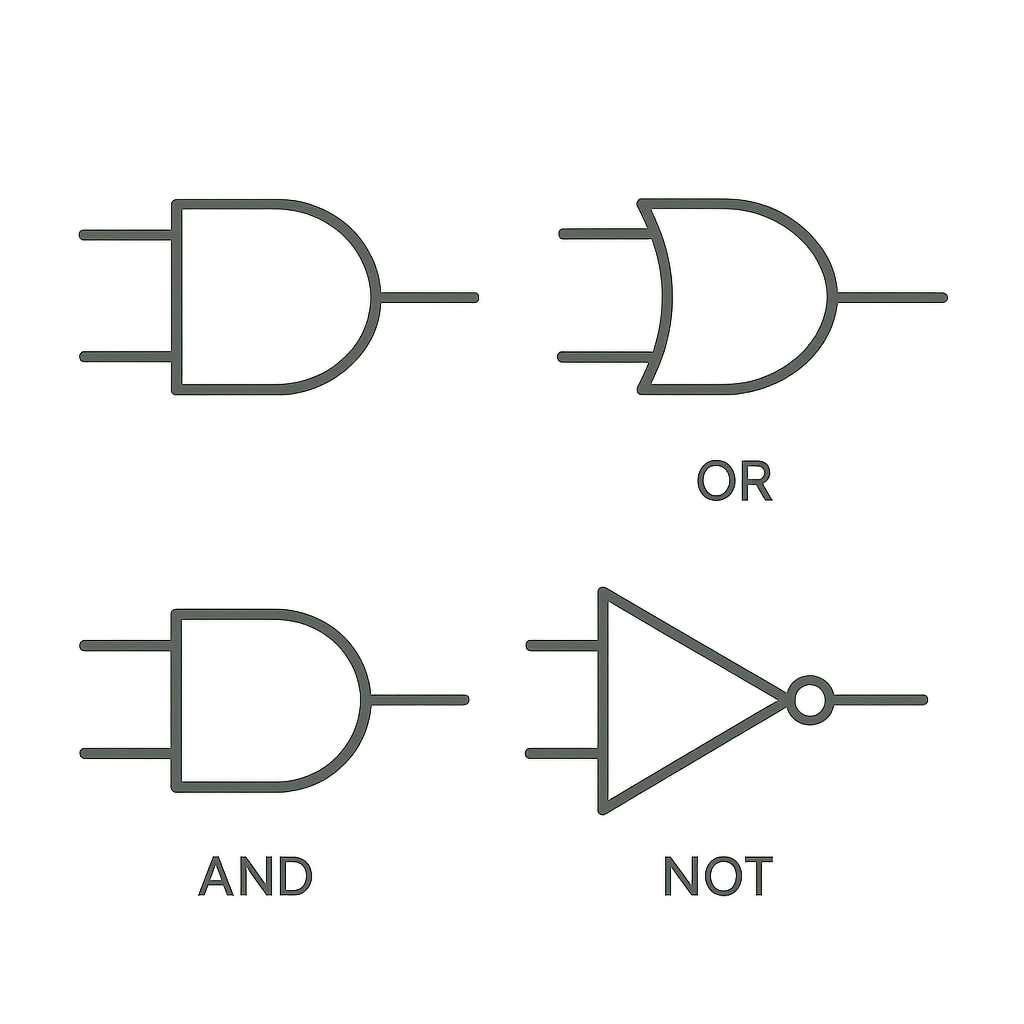
Einführung in die boolesche Algebra
Die boolesche Algebra ist ein Teilbereich der Mathematik, der sich mit den Werten wahr (1) und falsch (0) befasst. Sie ist nach dem Mathematiker George Boole benannt und bildet die Grundlage für digitale Schaltungen und Programmierung.
Grundoperationen
Es gibt drei grundlegende Operationen in der booleschen Algebra:
- AND: Gibt nur dann 1 zurück, wenn beide Eingaben 1 sind.
- OR: Gibt 1 zurück, wenn mindestens eine Eingabe 1 ist.
- NOT: Kehrt den Wert um; 1 wird zu 0 und umgekehrt.
Wahrheitstabellen
Wahrheitstabellen sind eine einfache Möglichkeit, die Ergebnisse der booleschen Operationen darzustellen. Hier sind die Wahrheitstabellen für die grundlegenden Operationen:
AND
A | B | A AND B
---|---|---------
0 | 0 | 0
0 | 1 | 0
1 | 0 | 0
1 | 1 | 1
OR
A | B | A OR B
---|---|--------
0 | 0 | 0
0 | 1 | 1
1 | 0 | 1
1 | 1 | 1
NOT
A | NOT A
---|-------
0 | 1
1 | 0
Komplexe Ausdrücke
Boolesche Ausdrücke können kombiniert werden, um komplexere logische Operationen zu erstellen. Zum Beispiel:
(A AND B) OR (NOT C)In solchen Fällen können Wahrheitstabellen helfen, die Ergebnisse zu ermitteln.
Anwendungen der booleschen Algebra
Die boolesche Algebra findet Anwendung in verschiedenen Bereichen:
- Digitale Schaltungen: Entwurf von Logikgattern.
- Programmierung: Logische Bedingungen in Code.
- Datenbanken: Abfragen und Filterungen.
Hinweis & Quellen
Dieser Guide basiert auf allgemein anerkannten Konzepten der booleschen Algebra und deren Anwendungen. Für vertiefte Informationen empfehlen wir die Literatur zur Mathematik und Informatik.